
การถ่ายเทความร้อนเกิดขึ้นได้อย่างไร ?
การถ่ายเทความร้อน (Heat Transfer)
ทุกคนรู้อยู่แล้วว่า ขวดน้ำเย็นจะอุ่นขึ้นถ้าเราวางทิ้งไว้ในที่ที่มีอากาศร้อน และถ้าเรานำขวดน้ำเย็นไปแช่ตู้เย็น น้ำก็จะเย็นขึ้น และเรายังรู้อีกว่าความร้อนจะส่งผ่านจากบริเวณที่มีอุณหภูมิสูง ไปสู่บริเวณที่มีอุณหภูมิต่ำ ปรากฏการณ์นี้ทางวิทยาศาสตร์เรียกว่า “การถ่ายเทความร้อน (Heat Transfer)”
กฎข้อที่ 1 ของเทอโมไดนามิกส์
กฎข้อที่ 1 ของเทอร์โมไดนามิกส์ (The first law of thermodynamics) รู้กันในหลักการที่ว่า “กฎการอนุรักษ์พลังงาน (Conservation of energy)” กล่าวว่า “พลังงานไม่มีทางถูกสร้างหรือสูญสลายเพียงแต่เปลี่ยนไปอยู่ในรูปของพลังงานอื่นเท่านั้น”
จากคำกล่าวนี้จึงเขียนสมการได้ว่า
(Ein) – (Eout) = (ΔEsystem)
- Ein = พลังงานที่ใส่ให้กับระบบ
- Eout = พลังงานที่ระบบปล่อยออกไป
- ΔEsystem = พลังงานที่เปลี่ยนแปลงในระบบ
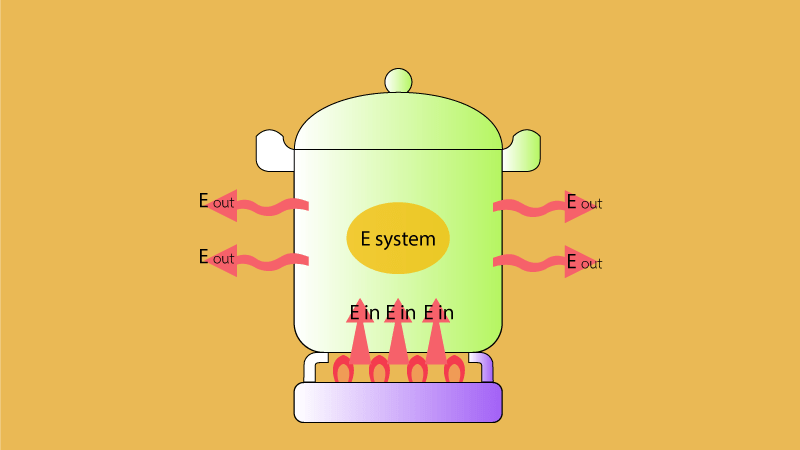
ภาพที่ 1 รูปที่อธิบายกฎการอนุรักษ์พลังงาน มีพลังงานเข้าพลังงานออกและการเปลี่ยนแปลง
สมดุลพลังงานสำหรับระบบปิด (Energy Balance for Close Systems)
ระบบปิด(Close Systems) หมายถึง ระบบที่มวลไม่เปลี่ยนแปลง เช่น กระป๋องน้ำอัดอุณหภูมิ 12°C วางไว้ที่อุณหภูมิห้อง 25°C เมื่อเวลาผ่านไป กระป๋องน้ำอัดลมอุณหภูมิเพิ่มขึ้นเป็น 20°C
จากตัวอย่าง กระป๋องน้ำอัดลมมีมวลของน้ำเท่าเดิมไม่เปลี่ยนไปจากตอนแรกที่ตั้งไว้ แต่ได้รับความร้อนจากภายนอกซึ่งมีอุณหภูมิสูงกว่า(25°C) จึงทำให้กระป๋องน้ำอัดลมอุณหภูมิสูงขึ้นเป็น 20°C (น้ำร้อนขึ้น)
เราสามารถเขียนสมการได้ว่า
(Ein) – (Eout) = (ΔEsystem)
ΔU = mcvΔT
หรือ
Q = mcvΔT
- ΔU = พลังงานของระบบที่เปลี่ยนแปลงไป หรือ ΔEsystem
- Q = พลังงานความร้อน (kJ)
- m = มวลของระบบ (kg)
- cv = ความจุความร้อนจำเพาะ (kJ/kg.K)
- ΔT = อุณหภูมิที่เปลี่ยนแปลงไป (K)

ภาพที่ 2 ภาพตัวอย่างที่เป็นกระป๋อง และการคำนวณ
สมดุลพลังงานสำหรับระบบเปิด (Steady-Flow System)
Steady-Flow System คือ ระบบที่มีการไหลคงที่มวลที่ไหลเข้าเท่ากับมวลที่ไหลออก เช่น ท่อน้ำประปามีน้ำไหลอยู่ภายในท่อ ซึ่งน้ำที่ไหลเข้าทางต้นท่อก็จะเท่ากับน้ำที่ไหลออกทางปลายท่อเช่นกัน ระบบนี้เรียกว่า Steady-Flow System
เราสามารถเขียนสมการได้ว่า
Q̇ = ṁcvΔT
- ΔU = พลังงานของระบบที่เปลี่ยนแปลงไป หรือ ΔEsystem
- Q̇ = อัตราการถ่ายเทพลังงานความร้อน (kJ/s)
- ṁ = อัตราการไหลของมวล (kg/s)
- cv = ความจุความร้อนจำเพาะ (kJ/kg.K)
- ΔT = อุณหภูมิที่เปลี่ยนแปลงไป (K)
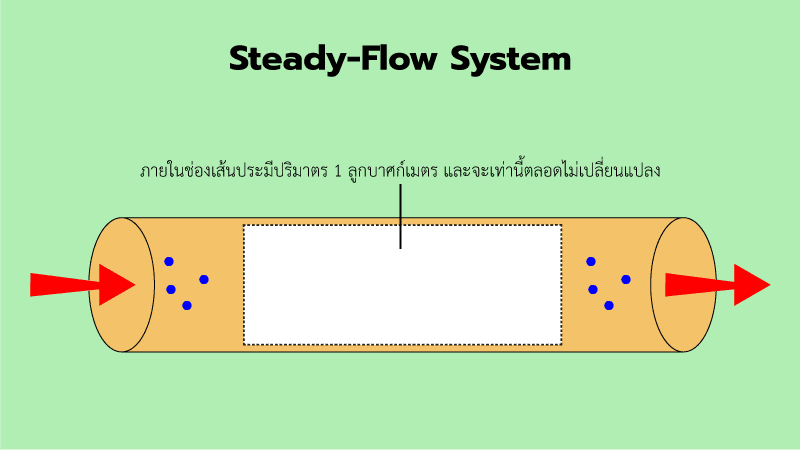
ภาพที่ 3 ภาพตัวอย่างการไหลภายในท่อ
รูปแบบของการถ่ายเทความร้อน (Heat Transfer Mechanisms)
การถ่ายเทความร้อนจากบริเวณหนึ่งสู่อีกบริเวณหนึ่ง สามารถทำได้ 3 วิธีคือ
- การนำความร้อน (Conduction)
- การพาคววามร้อน (Convection)
- การแผ่รังสีความร้อน (Radiation)
- การนำความร้อน (Conduction)
เป็นการส่งผ่านความร้อนซึ่งต้องอาศัยตัวกลาง (medium) ได้แก่ ของแข็ง (Solid), ของเหลว (Liquid) และ แก๊ส (Gas) โดยตัวกลางนั้น มีลักษณะอยู่นิ่ง รูปร่างคงที่
เช่น
- การใช้ตะเกียบโลหะคีบหมูกระทะ แล้วรู้สึกร้อนที่มือ เนื่องจากตะเกียบโลหะได้รับความร้อนและส่งความร้อนมาที่มือของเรา
- อากาศนิ่ง (Static Air) ซึ่งอยู่ระหว่างกระจกอาคาร ก็ถือว่าเป็นการนำความร้อนเช่นกัน

ภาพที่ 4 ภาพตัวอย่างอธิบายการนำความร้อน เป็นตะเกียบ+ไฟ
สัมประสิทธิ์การนำความร้อน (Thermal Conductivity or K-Value)
อย่างที่เรารู้กันอยู่ว่า ถ้าจะกินหมูกระทะเราควรใช้ตะเกียบไม้แทนที่จะใช้ตะเกียบโลหะ เพราะตะเกียบไม้จะไม่ร้อน ส่วนตะเกียบโลหะจะร้อน แล้วเรารู้ไหมว่า เพราะอะไร?
สิ่งที่ทำให้ตะเกียบทั้ง 2 ชนิดนี้แตกต่างกันคือค่าการนำความร้อน (K-Value) ซึ่งจะบอกว่าความร้อนสามารถส่งผ่านไปที่อีกฝั่งหนึ่งได้มากขนาดไหน ซึ่งจะขึ้นกับชนิดของวัสดุ
- ถ้ามีค่าสัมประสิทธิ์การนำความร้อนสูง หมายความว่า สามารถส่งความร้อนไปได้มาก
- ถ้าค่าสัมประสิทธิ์การนำความร้อนต่ำ หมายความว่า สามารถส่งผ่านความร้อนไปได้น้อย
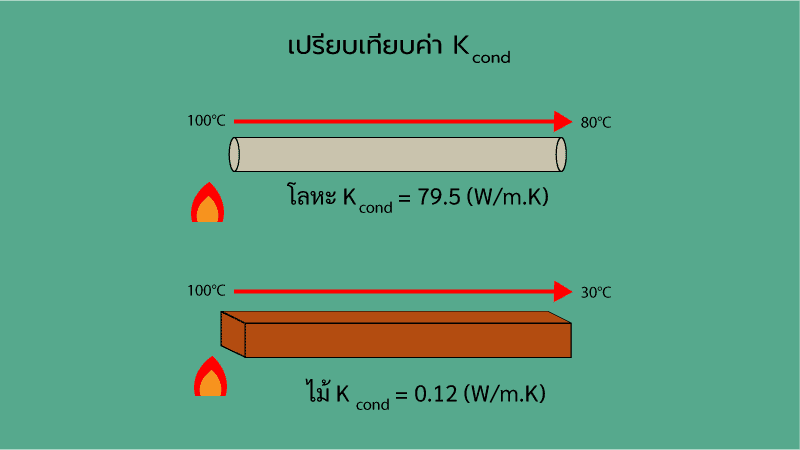
ภาพที่ 5 ภาพความแตกต่างระหว่างวัสดุที่มีค่าการนำความร้อนสูงกับต่ำ
จากตัวอย่างจึงสามารถบอกได้ว่า ตะเกียบ “โลหะ” มีค่าการนำความร้อนสูง ตะเกียบ “ไม้” มีค่าการนำความร้อนต่ำ
ซึ่งเราสามารถคำนวณหาอัตราการนำความร้อนได้จาก
Q̇cond = kcond x A x (T1 -T2) /Δx
- Q̇cond = อัตราการนำความร้อน (kJ/s)
- kcond = สัมประสิทธิ์การนำความร้อน
- A = พื้นที่ส่วนที่ถ่ายเทความร้อน (m2)
- T1 = อุณหภูมิที่ 1 (K)
- T2 = อุณหภูมิที่ 2 (K)
- Δx = ความหนาของตัวกลาง (m)

ภาพที่ 6 ตัวอย่างแสดงการคำนวณพร้อมภาพประกอบ
จากตัวอย่างนี้ เราจะเห็นได้ว่า ถ้าค่าสัมประสิทธิ์การนำความร้อนยิ่งต่ำ อุณหภูมิอีกฝั่งก็จะต่ำลง เราจึงมีตัวแปรอีกค่าหนึ่งที่เรียกว่า “สัมประสิทธิ์การต้านทานความร้อน (R-Value)”
สัมประสิทธิ์การต้านทานความร้อน (Thermal Resistance or R-Value)
ตัวแปรที่ตรงข้ามกับค่าสัมประสิทธิ์การนำความร้อน (K-Value)
- ถ้าสัมประสิทธิ์การต้านทานความร้อนสูง หมายถึง ตัวกลางนั้นยอมให้ความร้อนผ่านได้น้อย
- ถ้าสัมประสิทธิ์การต้านทานความร้อนต่ำ หมายถึง ตัวกลางนั้นยอมให้ความร้อนผ่านได้มาก
- การพาความร้อน (Convection)
กระบวนการพาความร้อนเป็นกระบวนการที่อาศัยตัวกลางที่มีการเคลื่อนที่ ได้แก่ ของเหลว (Liquid) และ แก๊ส (Gas) โดยส่วนที่มีอุณหภูมิสูงจะลอยตัวขึ้นด้านบน และส่วนที่อุณหภูมิต่ำลดตัวลงด้านล่างดั่งที่เคยได้ยินติดหูว่า “อากาศร้อนลอยตัวสูงขึ้น อากาศเย็นลอยตัวต่ำลง”
เช่น
- น้ำชาซึ่งต้มอยู่ภายในแก้ว เราจะเห็นใบชาหมุนวนในแนวดิ่ง
- ลมจากคอมเพรสเซอร์แอร์ ซึ่งค่อนข้างร้อน

ภาพการพาความร้อนในถ้วยชา
ซึ่งการพาความร้อนนั้นขึ้นอยู่กับลักษณะของการพาความร้อน ถ้าเป็นอากาศเย็น เราจะจำแนกได้เป็น
- Free Convection (Natural Convection)
- Force Convection
ตัวอย่าง ในวันที่อากาศร้อนมากและเราได้ไปออกกำลังกายมา ถ้าหากเราอยู่เฉยๆ เราเรียกว่า “Free Convection” แต่ถ้าเราบอกร้อน ไม่ไหวแล้วต้องเปิดพัดลมช่วย เราเรียกว่า “Force Convection”
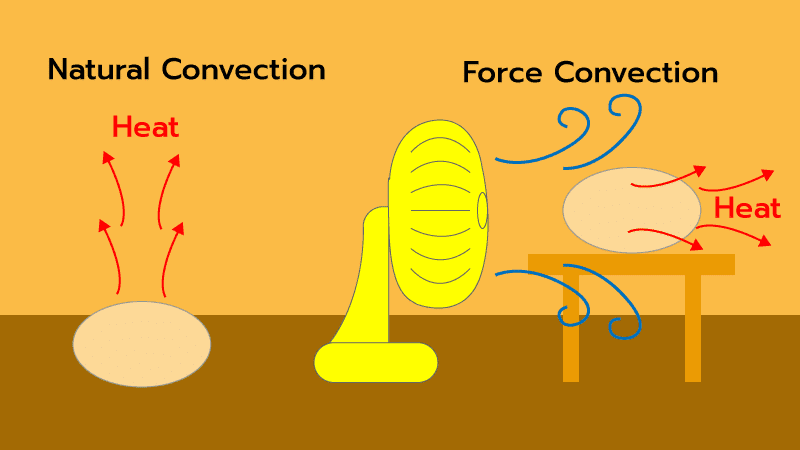
ภาพที่ 7 ภาพของ Free Convection และ Force Convection
สัมประสิทธิ์การพาความร้อน (Convection Coefficient)
ตัวแปรค่านี้เป็นส่วนที่บอกเราว่า สภาพแวดล้อม ณ ขณะนั้นสามารถพาความร้อนออกไปได้เท่าไหร่
- ถ้าสัมประสิทธิ์การพาความร้อนมีค่ามาก หมายความว่า ของไหลพาความร้อนออกไปได้มาก
- ถ้าสถ้าสัมประสิทธิ์การพาความร้อนมีค่าน้อย หมายความว่า ของไหลพาความร้อนออกไปได้น้อย

ภาพที่ 8 ภาพของไหลที่พาความร้อนออกไปได้มากน้อยต่างกัน
เราสามารถคำนวณอัตราความร้อนจากการพาความร้อนได้จาก Newton’s law of cooling
Q̇conv = hconv As (Ts -T∞)
- Q̇conv = อัตราการพาความร้อน (kJ/s)
- hconv = สัมประสิทธิ์การพาความร้อน
- As = พื้นที่ผิวส่วนที่เกิดการพาความร้อน (m2)
- Ts = อุณหภูมิผิววัตถุ (K)
- T∞ = อุณหภูมิของไหล (K)
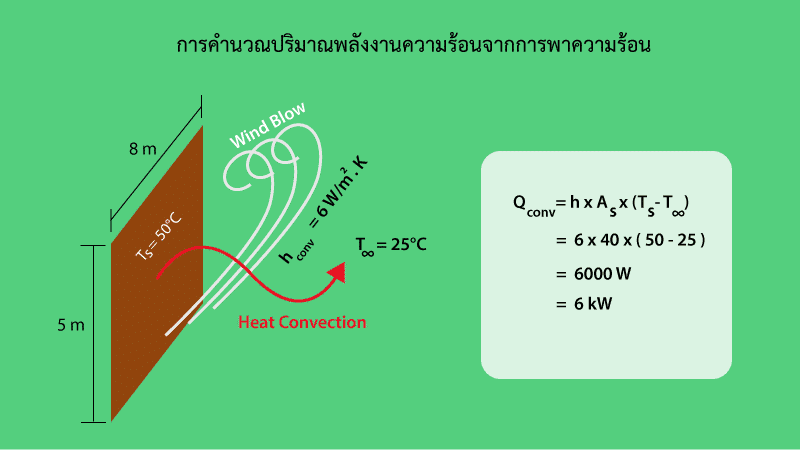
ภาพที่ 9 ภาพการคำนวณการพาความร้อน
จากตัวอย่างนี้เราสามารถบอกได้ว่า ปริมาณของความร้อนผ่านการพาความร้อนขึ้นอยู่กับค่าของ
- hconv ค่าสัมประสิทธิ์ของการพาความร้อน
- As พื้นที่ผิว
- T∞ อุณหภูมิของของไหล
- การแผ่รังสีความร้อน (Radiation)
การแผ่รังสีความร้อนเป็นการปล่อยพลังงานในรูปแบบของ คลื่นแม่เหล็กไฟฟ้า ซึ่งไม่ต้องอาศัยตัวกลาง สามารถเดินทางผ่านสุญญากาศได้
เช่น
- การแผ่รังสีของดวงอาทิตย์มาที่โลกผ่านอวกาศซึ่งเป็นสุญญากาศ
วัตถุทุกชนิดที่มีอุณหภูมิสูงกว่า 0 เคลวิล (K) จะมีการปล่อยรังสีความร้อนและดูดซับรังสีความร้อน เราสามารถคำนวณค่าการแผ่รังสีความร้อนได้จาก Stefan-Boltzmann law (กฎของสเตฟาน-โบลทซ์มานน์)
Q̇rad = εσAs T4s
- Q̇rad = อัตราการแผ่ความร้อน
- ε = สัมประสิทธิ์การแผ่ความร้อน
- σ = พื้นที่ผิวส่วนที่เกิดการพาความร้อน (m2)
- As = พื้นที่ผิวการแผ่รังสีความร้อน
- Ts = อุณหภูมิผิววัตถุ (K)
โดยปกติ ค่าสัมประสิทธิ์การแผ่รังสีความร้อนจะมีค่าน้อยกว่า 1 ส่วนวัตถุที่มีค่าสัมประสิทธิ์การแผ่รังสีความร้อนเท่ากับ 1 เราจะเรียกวัตถุนั้นว่า “วัตถุดำ หรือ Blackbody” และจะเป็นวัตถุที่มีค่าสัมประสิทธิ์การแผ่รังสีความร้อนมากที่สุด
การแผ่รังสีความร้อนเป็นการปล่อยพลังงานในรูปแบบของ คลื่นแม่เหล็กไฟฟ้า ซึ่งไม่ต้องอาศัยตัวกลาง สามารถเดินทางผ่านสุญญากาศได้
เช่น
- การแผ่รังสีของดวงอาทิตย์มาที่โลกผ่านอวกาศซึ่งเป็นสุญญากาศ
วัตถุทุกชนิดที่มีอุณหภูมิสูงกว่า 0 เคลวิล (K) จะมีการปล่อยรังสีความร้อนและดูดซับรังสีความร้อน เราสามารถคำนวณค่าการแผ่รังสีความร้อนได้จาก Stefan-Boltzmann law (กฎของสเตฟาน-โบลทซ์มานน์)
Q̇rad = εσAs T4s
- Q̇rad = อัตราการแผ่ความร้อน
- ε = สัมประสิทธิ์การแผ่ความร้อน
- σ = พื้นที่ผิวส่วนที่เกิดการพาความร้อน (m2)
- As = พื้นที่ผิวการแผ่รังสีความร้อน
- Ts = อุณหภูมิผิววัตถุ (K)
โดยปกติ ค่าสัมประสิทธิ์การแผ่รังสีความร้อนจะมีค่าน้อยกว่า 1 ส่วนวัตถุที่มีค่าสัมประสิทธิ์การแผ่รังสีความร้อนเท่ากับ 1 เราจะเรียกวัตถุนั้นว่า “วัตถุดำ หรือ Blackbody” และจะเป็นวัตถุที่มีค่าสัมประสิทธิ์การแผ่รังสีความร้อนมากที่สุด
สรุป
การส่งผ่านความร้อน (Heat Transfer) เป็นการส่งผ่านความร้อนจากบริเวณที่มีอุณหภูมิสูงกว่าไปสู่บริเวณที่มีอุณหภูมิต่ำกว่า โดยทำได้ 3 วิธี คือ
- การนำความร้อน
- การพาความร้อน
- การแผ่รังสีความร้อน
โดยที่การนำความร้อนและการพาความร้อนต้องอาศัยตัวกลางเพื่อส่งผ่านความร้อน ส่วนการแผ่รังสีความร้อนนั้นไม่ต้องใช้ตัวกลาง
การคำนวณเพื่อนำไปวิเคราะห์ข้อมูลทางความร้อนนั้นไม่สามารถใช้อย่างใดอย่างหนึ่งได้ เพราะในความเป็นจริงการถ่ายเทความร้อน เกิดทั้ง 3 รูปแบบพร้อมกัน และอยู่ในรูปแบบของ 3 มิติ (ทุกทิศทาง) ซึ่งเป็นเรื่องที่ท้ายทายอย่างมาก
แต่การมีความรู้พื้นฐานที่ถูกต้องก็สามารถนำไปวิเคราะห์และ คาดการณ์ได้อย่างเป็นเหตุเป็นผลนับว่ามีประโยชน์อย่างมาก
Source : Heat and Mass Transfer fundamentals & Application fifth edition Book
ติดตามข่าวสาร
- Facebook : https://www.facebook.com/3tinsulation/
- Website : https://3t-insulation.com/
